Вычислительные комплексы и сети. Лекции

Страница 28	Вычислительные комплексы и сети. Лекции
Главная Страница 1 Страница 2 Страница 3 Страница 4 Страница 5 Страница 6 Страница 7 Страница 8 Страница 9 Страница 10 Страница 11 Страница 12 Страница 13 Страница 14 Страница 15 Страница 16 Страница 17 Страница 18 Страница 19 Страница 20 Страница 21 Страница 22 Страница 23 Страница 24 Страница 25 Страница 26 Страница 27 Страница 28 Страница 29 Страница 30 Страница 31 Страница 32 Страница 33 Страница 34 Страница 35 Страница 36 Страница 37 Страница 38 Страница 39 Страница 40 Страница 41 Страница 42 Страница 43 Страница 44 Страница 45 Страница 46 Страница 47 Страница 48 Страница 49 Страница 50 Страница 51 Страница 52 Страница 53 Страница 54 Страница 55 Страница 56 Страница 57 Страница 58 Страница 59 Страница 60 Страница 61 Страница 62 Страница 63 Страница 64 Страница 65 Страница 66 Страница 67 Страница 68 Страница 69 Страница 70 Страница 71 Страница 72 Страница 73 Страница 74 Страница 75 Страница 76 Страница 77 Страница 78 Страница 79 Страница 80 Страница 81 Страница 82 Страница 83 Страница 84 Скачать учебник	Предыдущая страница	Следующая страница
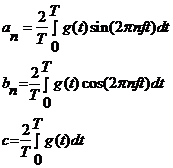
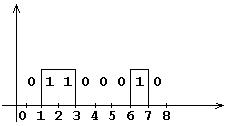
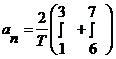
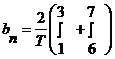
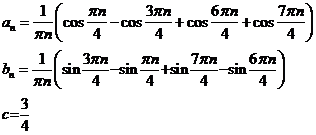
	- частота периодической функции T – период. - амплитуды синусов и косинусов n-ой гармоники c = const; Разложенная на гармоники функция может быть восстановлена, если период T и амплитуды гармоник известны. Пример: Интегрируем: 1 гармоника – при n = 1 2 гармоника – при n = 2 … и т.д. Если ось ОУ: - среднеквадратичное отклонение амплитуды, которое характеризует энергию, передаваемую n-ой гармоникой на частоте f. 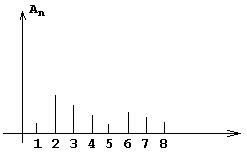Восстанавливаем g(t):
	Предыдущая страница	Следующая страница

Страница 28

Вычислительные комплексы и сети. Лекции