Страница 43

Вычислительные комплексы и сети. Лекции

2)      Кодовое расстояние. Количество битов, которыми различаются 2 кодовых слова. Для получения кодового расстояния между кодовыми словами их надо сложить по модулю 2 и сосчитать количество единиц. Например, 1000101 – первое кодовое слово, и 1011001 – второе. Результат – 0011100. Кодовое расстояние равно 3. Смысл кодового расстояния заключается в следующем. Если 2 кодовых слова находятся на кодовом расстоянии t, то для преобразования одного кодового слова в другое потребуется d единичных ошибок. Если кодовое слово длиной m+k, то 2^m – количество допустимых комбинаций (информационных сообщений). Не все допустимые информационные сообщения при появлении ошибок будут входить в 2ⁿ число сообщений. При этом контрольные разряды формируются по определённому алгоритму. Зная алгоритм формирования контрольных разрядов, можно построить полный список всех допустимых кодовых слов. При этом в этом списке можно найти такую пару кодовых слов, кодовое расстояние между которыми будет минимальным. Это расстояние называется минимальным кодовым расстоянием. Обычно обозначается d_min. Способность алгоритма кодирования по обнаружению и исправлению ошибок зависит от минимального кодового расстояния.

Вывод:

Не все значения кодовых слов 2^n=m+k являются допустимыми.

Пример обнаружения ошибки: применяют кодирование с контрольным разрядом или контроль на чётность. Бит чётности формируется таким образом, чтобы количество единиц в кодовом слове было чётным.

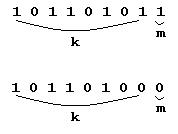
10110101 – m информационных бит, 1 – k контрольных бит. Минимальное кодовое расстояние равно d_min=2. При приёме осуществляется подсчёт единиц и сравнение полученной суммы с контрольным разрядом. Если количество единиц нечётное, то произошла ошибка. Где – неясно.

Исправление ошибки: Предположим. Допустимые комбинации следующие:

1)      0 0 0 0 0 0 0 0 0 0

2)      0 0 0 0 0 1 1 1 1 1

3)      1 1 1 1 1 0 0 0 0 0

4)      1 1 1 1 1 1 1 1 1 1

d_min = 5. Если получено сообщение R = 0000000111 – ошибка, такого допустимого кодового слова нет, количество исправленных ошибок подсчитывается по формуле

. Поэтому на приемном конце будет сделан вывод о том, что передавалось 0000011111. Но возможен вариант, когда передавались 00…00 и произошла тройная ошибка, тогда исправление будет неверным – ошибка декодирования.

Код Хемминга

В общем случае различают 2 типа кодирования:

1. Кодирование источников. При этом кодировании избыточность сообщения снижается, и такое кодирование называется сжатием данных.
2. Кодирование каналов.

Примеры кодирования источников: код Морзе, оцифровка аудио сигнала, код Хаффмана, и т.п.

Опр. Кодирование канала – процесс увеличения избыточности сообщения путем внесения проверочных символов, позволяющие обнаружить или исправить ошибку, возникающую при передаче информации.

Опр. Кодом называется 4-ка объектов (A,B,F,E), где A – множество информационных слов, B – множество кодовых слов, F – отображение A на B (
) – кодер, E – отображение множества значений B на множество A (
) – декодер. То есть любой код формально можно определить, как C = (A,B,F,E).